Everyone learns (and some readers maybe still remember) the quadratic formula. It’s a pillar of algebra and allows you to solve equations like Ax2+Bx+C=0. But just because you’ve used it doesn’t mean you know how to come up with the formula itself. It’s a bear to derive so the vast majority of us simply memorize the formula. A Carnegie Mellon mathematician named Po-Shen Loh didn’t expect to find a new way to derive the solution when he was reviewing math materials for middle school use to make them easier to understand. After all, people have been solving that equation for about 4,000 years. But that’s exactly what he did.
Before we look at the new solution, let’s talk about why you want to solve quadratic equations. They are used in many contexts. In ancient times you might use them to determine how much more crop to grow to cover pay tax payments without eating in to the crop you needed to subsist. In physics, it can describe motion. There’s seemingly no end to how many things you can describe with a quadratic equation.
Babylonians, in particular, would solve simultaneous equations to find the roots of a quadratic. Egyptians, Grecians, Indians, and Chinese peoples used graphical methods to solve the equations. The entire history is a bit much to get into, but still a great read. For this article, let’s dig into how the new derivation was discovered.
Setting Up the Equation
So what’s the method? You watch Loh explain it himself in the video, below. Suppose you have a standard quadratic equation for whatever reason that looks like this:
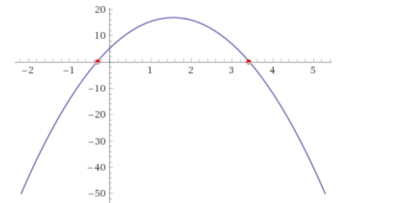
x2-6x+3=0
In this case, A=1, B=6, and C=3. Note that for Loh’s method to work, A should equal 1, but if it doesn’t you can always divide both sides by A to make that true. For example, consider this equation:
3x2-18x+9=0
It will have the same roots as the first one because if you divide both sides by 3, you get the first equation.
The Polynomial Factor
To factor a polynomial into two binomials we can use FOIL (First/Inner/Outer/Last). So we know that:
x2-6x+3=(x-S)(x-R)
Where we just made up S and R. They exist, but we don’t know what they are yet. However, for the answer to be zero, you can see that the equation will be zero when x=S or X=R so that means S and R are the roots of the equation.
So What’s S and R?
It sounds silly, but let’s multiply out the binomials into another polynomial. Remember FOIL:
x2-6x+3=x2-(S+R)x+SR
If you look at that for a second, you will probably realize that S times R must be 3. We also know they add up to 6. At this point, you can probably just guess the roots, but let’s make it formal.
The roots of a polynomial like this will be in the form of U±z. So if S=U+z and R=U-z, the only way to make (U+z)+(U-z) equal to 6 is if U is 6/2. Since B is -6 in this example, we can intuit that U must …read more
Source:: Hackaday